A PID Controller (Proportional-Integral-Derivative Controller) is a widely used control system mechanism that continuously calculates an error value and applies a correction based on proportional, integral, and derivative terms. It is commonly used in industrial automation, robotics, and process control systems.
1. How Does a PID Controller Work?
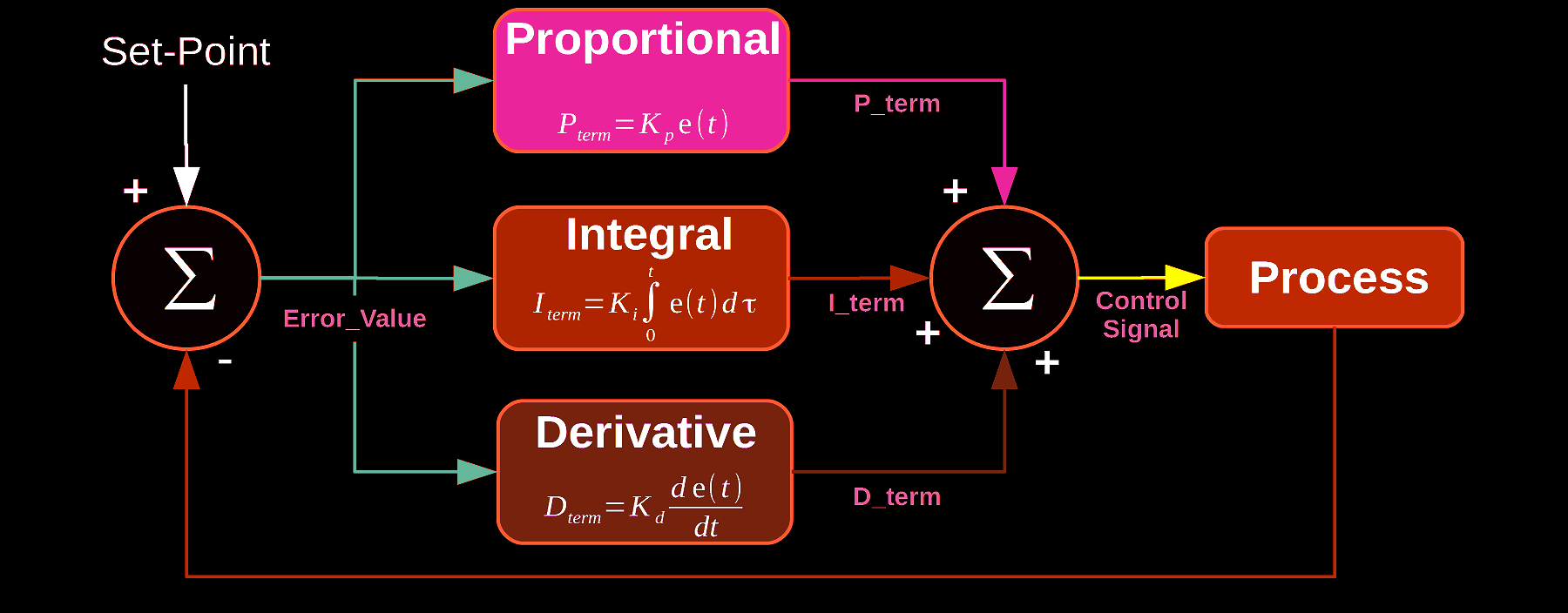
A PID controller works by minimizing the difference between a desired setpoint (SP) and the measured process variable (PV). This difference is called the error (e): e(t)=SP−PVe(t) = SP – PV
The controller then applies three corrective actions to adjust the system’s output:
- Proportional Control (P) – Reacts to the current error.
- Integral Control (I) – Reacts to the accumulated past error.
- Derivative Control (D) – Reacts to the rate of change of the error.
The control output is calculated as: u(t)=Kpe(t)+Ki∫e(t)dt+Kdddte(t)u(t) = K_p e(t) + K_i \int e(t) dt + K_d \frac{d}{dt} e(t)
Where:
- KpK_p = Proportional gain (determines response speed)
- KiK_i = Integral gain (eliminates steady-state error)
- KdK_d = Derivative gain (reduces overshoot and improves stability)
2. Breakdown of PID Components
(a) Proportional Control (P)
- Provides a correction proportional to the error.
- The larger the error, the stronger the correction.
- Improves response speed but does not eliminate steady-state error.
P=Kpe(t)P = K_p e(t)
Effect of Increasing KpK_p:
- Too low: Slow response.
- Too high: Oscillations or instability.
(b) Integral Control (I)
- Eliminates steady-state error by accumulating past errors.
- Slow response, but essential for precision.
I=Ki∫e(t)dtI = K_i \int e(t) dt
Effect of Increasing KiK_i:
- Too low: Residual error remains.
- Too high: Causes oscillations and overshoot.
(c) Derivative Control (D)
- Predicts future errors by measuring the rate of change.
- Improves stability and reduces overshoot.
D=Kdddte(t)D = K_d \frac{d}{dt} e(t)
Effect of Increasing KdK_d:
- Too low: System reacts too slowly.
- Too high: Causes excessive damping, reducing responsiveness.
3. PID Tuning: Adjusting Kp,Ki,KdK_p, K_i, K_d
Tuning a PID controller means selecting the right values for Kp,Ki,KdK_p, K_i, K_d to achieve optimal performance.
Tuning Methods
- Ziegler-Nichols Method (Experimental approach)
- Trial and Error (Manually adjusting parameters)
- Software-based Optimization (Using MATLAB, Simulink, or other tools)
- Auto-tuning Algorithms (Found in modern industrial controllers)
Effects of Tuning
| Parameter | Too Low | Too High |
|---|---|---|
| KpK_p (Proportional) | Slow response | Overshoot & oscillations |
| KiK_i (Integral) | Steady-state error | Excessive oscillations |
| KdK_d (Derivative) | Slower reaction | Unstable system |
4. Applications of PID Controllers
PID controllers are used in various industries for precise control of dynamic systems.
Industrial & Engineering Applications
- Temperature Control: Ovens, HVAC, water heaters
- Motor Speed Control: Robotics, CNC machines, electric vehicles
- Level Control: Water tanks, chemical reactors
- Pressure Control: Industrial manufacturing, power plants
- Position Control: Servo motors, robotic arms, drones
Everyday Applications
- Cruise Control: In cars to maintain constant speed
- Autopilot Systems: Aircraft flight control
- Drones & Robotics: Maintaining balance and movement
5. Types of PID Controllers
Depending on the application, PID controllers can be used in different configurations:
- P Controller: Uses only proportional control (fast but inaccurate).
- PI Controller: Uses proportional and integral control (eliminates steady-state error).
- PD Controller: Uses proportional and derivative control (faster response, reduced overshoot).
- Full PID Controller: Uses all three terms (best stability and accuracy).

7. Advantages & Disadvantages
✅ Advantages
✔ Simple and widely used
✔ No need for a system model
✔ Works well for many applications
❌ Disadvantages
✖ Requires tuning for each application
✖ Can become unstable if not tuned properly
✖ Not ideal for highly dynamic, nonlinear systems
Leave a Reply